Cara Hitung Manual Prediksi Metode Regresi Linier di Excel
Assalamualaikum, Wr. Wb, Salam Rahayu dan Salam Budaya
Dalam dunia statistika, analisis regresi linier sederhana adalah salah satu teknik yang digunakan untuk memahami hubungan antara dua variabel. Metode ini dapat membantu kita dalam melakukan prediksi atau pemodelan berdasarkan data yang ada. Dalam artikel ini, kita akan menjelajahi konsep regresi linier sederhana dengan menggunakan bahasa yang lebih mudah dipahami oleh mahasiswa.
Pengertian Regresi Linier Sederhana:
Regresi linier sederhana merupakan metode statistika yang digunakan untuk mempelajari hubungan antara dua variabel: variabel independen (X) dan variabel dependen (Y). Tujuan utama regresi linier sederhana adalah untuk menemukan garis lurus terbaik yang dapat menggambarkan hubungan antara kedua variabel tersebut.
Bagaimana Regresi Linier Sederhana Bekerja:
Regresi linier sederhana menggunakan persamaan garis lurus (y = bx + a) untuk menggambarkan hubungan antara X dan Y. Dalam persamaan ini, y adalah variabel dependen, x adalah variabel independen, m adalah kemiringan garis (koefisien regresi), dan c adalah perpotongan garis dengan sumbu Y (konstanta).
Langkah-langkah Analisis Regresi Linier Sederhana:
- Pengumpulan Data: Pertama, kita perlu mengumpulkan data yang terkait dengan variabel X dan variabel Y. Misalnya, jika kita ingin memahami hubungan antara jam belajar (X) dan nilai ujian (Y), maka kita perlu mengumpulkan data tentang jam belajar dan nilai ujian siswa.
- Membuat Scatter Plot: Setelah mengumpulkan data, langkah berikutnya adalah membuat scatter plot. Scatter plot adalah grafik yang menunjukkan titik-titik data pada koordinat kartesian, dengan variabel X di sumbu horizontal dan variabel Y di sumbu vertikal. Grafik ini membantu kita untuk memvisualisasikan hubungan antara kedua variabel.
- Menemukan Garis Regresi: Setelah membuat scatter plot, kita perlu menemukan garis regresi yang terbaik untuk mewakili hubungan antara X dan Y. Garis regresi ini merupakan garis lurus yang terdekat dengan sebanyak mungkin titik data pada scatter plot. Metode umum yang digunakan untuk menemukan garis regresi adalah metode least squares.
- Menafsirkan Hasil: Setelah menemukan garis regresi, kita dapat menafsirkan hasilnya. Koefisien regresi (m) memberikan informasi tentang seberapa besar perubahan dalam variabel dependen (Y) yang diharapkan ketika variabel independen (X) berubah satu unit. Konstanta (a) memberikan nilai prediksi Y ketika X sama dengan nol.
- Menguji Signifikansi Statistik: Selain itu, kita juga dapat menguji signifikansi statistik hubungan antara X dan Y.
Baca Juga : Cara menghitung confusion matrix multiclass 3x3
Sekarang kita akan membahas tutorial penggunaan Microsoft Excel untuk melakukan Analisis Regresi Linier Sederhana. Excel adalah salah satu perangkat lunak spreadsheet yang populer dan dapat membantu kita melakukan berbagai analisis statistik dengan mudah. Dalam tutorial ini, kita akan mempelajari langkah-langkah praktis untuk melakukan analisis regresi linier sederhana menggunakan Excel. Jadi, mari kita mulai dan pelajari cara menggunakan Excel untuk memahami hubungan antara dua variabel melalui analisis regresi linier sederhana.
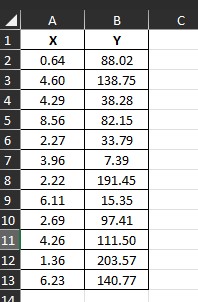
Contoh Data Tabel
untuk menentukan prediksi maka kita akan memerlukan persamaan (y = bx + a) maka untuk langkah pertama kita perlu mencari nilai b dan nilai konstanta atau a.
Rumus untuk mencari nilai b adalah :
b = (n * Σ(XY) - ΣX * ΣY) / (n * Σ(X^2) - (ΣX)^2)
agar tidak bingung maka kita bisa memisahkan masing-masing komponen diatas seperti ini :
- n adalah jumlah pasangan data (jumlah observasi).
- Σ(XY) adalah jumlah dari perkalian setiap nilai X dengan nilai Y yang sesuai.
- ΣX adalah jumlah dari semua nilai X.
- ΣY adalah jumlah dari semua nilai Y.
- Σ(X^2) adalah jumlah dari kuadrat setiap nilai X.
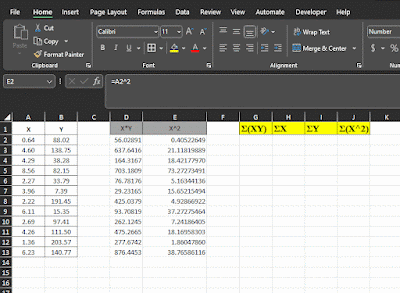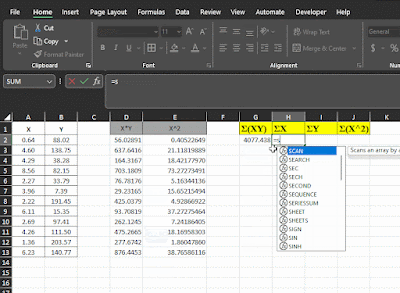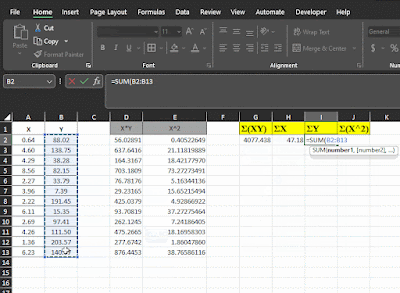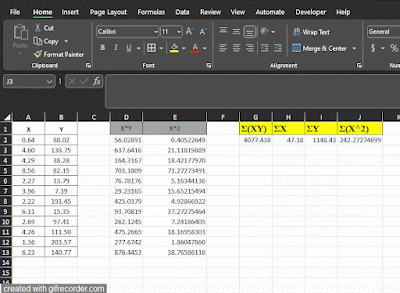
Kalau menggunakan excel maka gunakan tabel bantu seperti ini dan simak cara menghitungnya
Nah, setelah kamu berhasil menghitung dengan menggunakan tabel bantu diatas maka, Kemudian kamu tentukan nilai Σ nya dengan menggunakan formula atau rumus =SUM() seperti tampilan dibawah ini
Nah dari nilai-nilai Σ yang sudah diketahui maka, kamu masukkan kedalam rumus
- n = 12
- Σ(XY) = 4077.438
- ΣX = 47.18
- ΣY = 1148.43
- Σ(X^2) = 242.2727